逐次モンテカルロ/(粒子|パーティクル|モンテカルロ)フィルタを実装してみた
このポストの概要
逐次モンテカルロ/粒子(パーティクル)フィルタとは
逐次モンテカルロ法 (Sequential Monte Carlo: SMC)/粒子フィルタ(Particle Filter)は、線形状態空間モデルに対してはカルマンフィルタを使うように、非線形状態空間モデルに対して状態変数の推定を行うアルゴリズムです。具体的には状態変数に対する確率分布をモンテカルロ法で生成したサンプルで近似する手法です。更なる別名としてSampling/Importance resampling (SIR)とも呼ばれているようです。またまた、Sequential Importance Sampling(SIS)なる別のアルゴリズムもあって、これは逐次モンテカルロ法における"リサンプリング処理"というモンテカルロで生成したサンプルに対するリサンプリング処理がない版になります(参照:粒子フィルタ - Wikipedia、英語版のほうがいいかも)。
名称が多数あってややこしいので、以下ではSMCに統一する方向で。
Rでの実装はあるんかい?
Rから使えそうなSMCの実装としては
あたりがある。なお、正確にはRcppSMCはC++のライブラリに処理をブン投げるという意味でRでの実装ではないです。またSMCパッケージは3年前に更新が止ってるのでアレ感ありますね、アレ感。
SMCを含めた状態空間モデルの平易なテキストとしては
が超お勧め。6章に粒子フィルタの解説が載っており、ここのコードもだいたいそれ見て実装してる。
また、特に(線形)状態空間モデルについては、以下のスライドがまとまっていて、大変ありがたいのでこれも見ておくといいかと。
の説明がかなり詳しい。
・・・で、私がお勉強用に作ったSMCの実装のコアの部分は以下(particle.filter関数)。コメント含め28行です。短く書けるのは良いことです。
一応、多次元系列データも扱えるように作ってはいるが、ちゃんと試してはいない。
particle.filter <- function(x0, size.particle, size.dim, size.data, system.equation, likelihood, lag=0) { total.loglikelihood <- 0 #dimension index : paricle * dimension * lag dims <- c(size.particle, size.dim, lag+1) x0 <- array(c(rep(x0, each=size.particle),rep(NA, size.dim*size.particle*lag)), dims) x <- array(rep(NA, size.particle*size.dim*(lag+1)), dims) dimnames(x0) <- make.name(size.particle, size.dim, lag) dimnames(x) <- make.name(size.particle, size.dim, lag) states <- vector("list", size.data) for( t in 1:size.data) { #Prediction : p(x_{t}|x_{t-1}) for(index.particle in 1:size.particle) { x[index.particle,, 1] <- system.equation(x0[index.particle,,1]) x[index.particle,,-1] <- x0[index.particle,,-(lag+1)] } #Likelihood : p(y_{t}|y_{1:t}) w <- apply(x, 1, function(z){likelihood(t, z[,1])}) total.loglikelihood <- total.loglikelihood + log(sum(w)/size.particle) #Weight ' resampling index <- resampling(w/sum(w)) #Filtering : p(x_{t}|y_{t}) x0 <- x[index,,,drop=FALSE] states[[t]] <- make.state(t, w, x, x0) } list(loglikelihood=total.loglikelihood, size=c(particle=size.particle, data=size.data, dim=size.dim,lag=lag), states=states) }
実行結果
とりあえず正しく動作しているのかを確認したかったので、答え合わせのしやすい線形状態空間モデルの例として以下のモデル
状態方程式:
観測方程式:
を使用。パラメーターとしてここでは,
と設定してます。
このモデルをRで書くと以下のようになって、モデル固有な部分はsystem.equation関数とlikelihood関数に全部押しつけるように設計してます。また、lag<-10となっている箇所は、固定ラグ平滑化の固定ラグのサイズ指定に相当します。つまり、固定ラグ平滑化のラグは10をMAXとして取っているということです。
# x_t = x_{t-1} + v_t, v_t \sim N(0, (\alpha*\sigma)^2) # y_t = x_t + w_t, w_t \sim N(0, \sigma^2) #という状態空間モデルの生成 make.system.equation <- function(alpha, sigma) { function(x) { v <- rnorm(length(x), sd=alpha*sigma) x + v } } make.likelihood.function <- function(y, sigma) { function(t, x) { 1/(sqrt(2*pi)*sigma)*exp(-(y[t,]-x)^2/(2*sigma^2)) } } sigma <- 1.0 alpha <- 0.8 set.seed(100) #データは100要素をもつ1系列として設定 size.data <- 100 #1000粒子用意 size.particle <- 1000 #真の状態変数系列xを作成 x.true <- cumsum(alpha*sigma*rnorm(size.data)) #そこにノイズをのっけて観測系列yを作成 y <- matrix(sigma*rnorm(size.data)+x.true) #状態方程式&観測方程式(尤度で表現)を生成 system.equation <- make.system.equation(alpha, sigma) likelihood <- make.likelihood.function(y, sigma) #SMCを適用 lag <- 10 pf <- particle.filter(rnorm(1), size.particle, 1, size.data, system.equation, likelihood, lag=lag)
粒子ごとに状態変数xの推定値が違うので、この結果をなんらかの手段(平均など)を用いて集約せんといかんわけです。そこで、各時点ごとの集約を実行するための関数としてaggregate.pf関数を用意したんでそれを使うことにします。この関数は、デフォルトでは各時点での粒子の状態の平均値を計算するようになってます。
#各粒子の算出した状態変数を集約(平均) x.pf <- aggregate.pf(pf, "filter", lag=0) x.pf.lag <- aggregate.pf(pf, "filter", lag=lag)
この結果(ラグなし&10ラグの固定ラグ平滑化)を描画すると以下のようになります。
ここでラグ付の結果を調整して通常のフィルタリングと時点を合わせるために適当な処理(c(x.pf.lag[-(1:lag)], rep(NA, lag))))が入っています。
matplot(cbind(x.pf, c(x.pf.lag[-(1:lag)], rep(NA, lag))), type="l",lty=1)
更にこれらを真の状態変数(x.true)と重ねて描画すると
matplot(cbind(x.true, x.pf, c(x.pf.lag[-(1:lag)], rep(NA, lag))), type="l",lty=1) legend("topleft", c("X(true)", "X(filter)", "X(fixed lag)"), col = c("black", "red", "green"), lty=1)
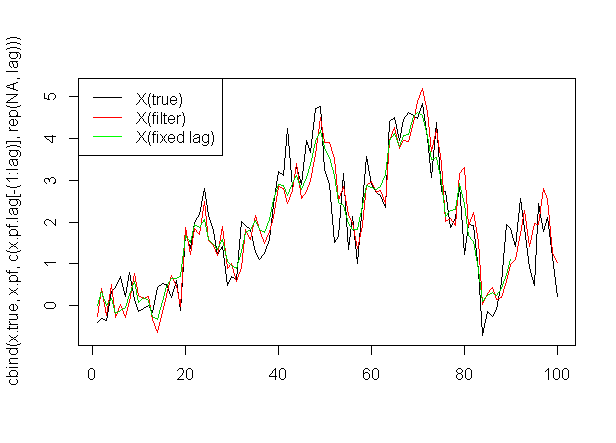
という感じ。あってる・・・?のかは判断しにくいので別の手段を考えます。
これがある程度妥当な結果かどうか確かめるため、ここで作成したモデルは線形状態空間モデル+ノイズはガウシアンってことで、カルマンフィルタでも計算できるので昔メモっといたカルマンフィルタの記事にならって、FKFパッケージってのを使って同じモデルのフィルタリングを実行してみる。カルマンフィルタのパッケージにどういうのがあるのかを知りたい場合には上述のスライドを見るか、State Space Models in R(PDF)を読むとよい。これを読む限りFKFはマイナーパッケージぽいが、まぁ答え合わせに使う分にはいいだろと。
同モデルをFKFパッケージのカルマンフィルタにかけるには以下のように書く。
#カルマンフィルタとの比較 library(FKF) dt <- matrix(0) ct <- matrix(0) Zt <- matrix(1) Tt <- matrix(1) a0 <- 0 P0 <- matrix(0.01) fkf.obj <- fkf(a0, P0, dt, ct, Tt, Zt, HHt=matrix((alpha*sigma)^2), GGt=matrix(sigma^2), yt = t(y))
この結果をSMCの結果とあわせて描画してみると
plot(y) lines(fkf.obj$att[1, ], col = "blue") lines(x.pf, col = "red") legend("bottomright", c("original data", "filter(Kalman)", "filter(PF)"), col = c("black", "blue", "red"), lty=1)

赤線(SMC)と青線(カルマンフィルタ)がほぼ重なっており、俺俺SMC実装は合っていそうだなということがわかる。やったね!
Rの全コード
とりあえずGistにUPしておいた。そのうちまとめるかも?
その他の参考スライド
- Data assim r
- 時系列解析の使い方 - TokyoWebMining #17
- http://heartruptcy.blog.fc2.com/blog-entry-90.html
- Particle Filter(中野先生、PDF)
- モンテカルロ・フィルタおよび平滑化について(北川先生、PDF)
特に@xiangze氏のスライドに関してはGitHub - xiangze/particlefilter_dynamical: particle filter sample of dynamical systems in Rに実装がアップされているので、こちらも勉強になる。また、@berobero11氏のBLOGポストはRStanを活用しつつ、さきほど紹介したテキスト「予測にいかす統計モデリングの基本」の内容を忠実に再現したものなので一読の価値あり。また、数式数式したい方は中野/北川先生の資料を見るといいんじゃなかろうか。
