EMアルゴリズムによる混合分布のパラメーター推定の解析計算＆実装例 from 「Rによるモンテカルロ法入門」

問題設定

R言語の書籍「Rによるモンテカルロ法入門」

のEMアルゴリズムに関連した「練習問題5.14」をpthonの練習がてらEMアルゴリズム構築までの数式もメモりながら解いてみたというお話。問題設定としては

$X_i \sim \theta g(x) + (1-\theta) h(x), (i=1...n)$

という混合分布(分布 $g(x)$ から確率 $\theta$ 、分布 $h(x)$ から確率 $1-\theta$ でサンプリング)から $n$ 個サンプリングした状況を考えて、このパラメーター $\theta$ をEMアルゴリズムで推定するというもの。機械学習の分野でいう所の「教師なし２クラス分類」に該当する（たぶん）。

グラフを使ってもうちょっとちゃんと説明しておくと、実際に観察された青い棒グラフで示されているデータ $x_i,(i=1...n)$ は赤色のグラフで示されている $h(x)$ からのサンプルなのか、それとも緑色のグラフで示されている $g(x)$ からのサンプルなのかを識別するための閾値的な量になっている $\theta$ というパラメーターを推定してましょうと、そして、既存のデータは $g(x),h(x)$ のどちらの分布から来た可能性が高いのかを判断しましょうとそういう問題。

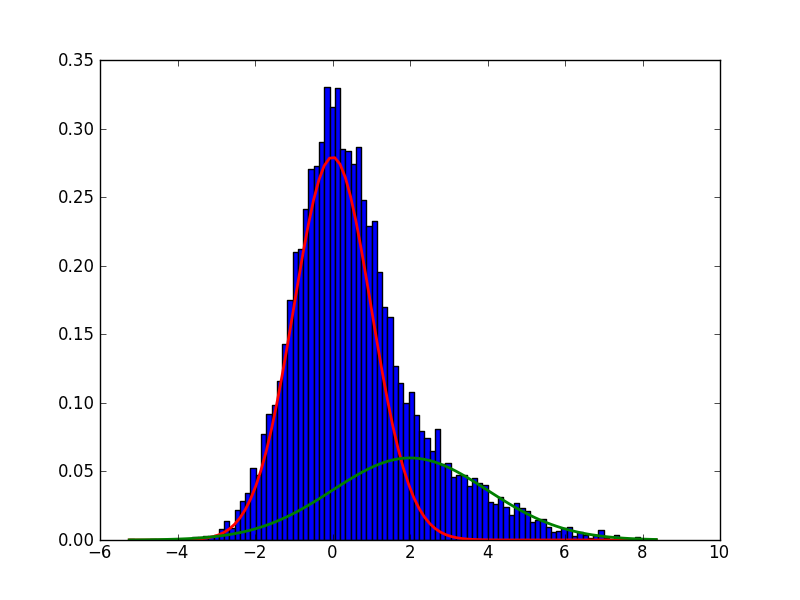
(縦軸：確率密度・横軸：確率変数 $X$ の実現値)

隠れ変数の導入

確率変数 $X_i$ の実現値 $x_i$ のみを取得した状況下ではこの $x_i$ が $g(x),h(x)$ のどちらの分布からのサンプルかは判断できないので、それを表わすために以下のような確率変数 $Z_i$ を各 $X_i$ に対応させる形で新たに導入する。

$Z_i:\Omega \rightarrow \{0,1\},(i=1...n)$

ただし

$P(Z_i=1)=\theta, P(Z_i=0) = 1-\theta,(i=1...n)$ （確率変数 $Z_i$ に測度を付与）
$X_i|Z_i=1 \sim g(x), X_i|Z_i=0 \sim h(x)$ （確率変数 $X_i$ の分布を指定）

とする。この $\{Z_i\}_{(i=1...n)}$ は実際には観測されないので欠損データor隠れ変数or潜在変数等と呼ばれる。以下 $X,x$ 等と添え字 $i$ なしに書いた場合、全確率変数orデータの集合を表しているものとする。つまり
$X := \{X_i\},(i=1...n)$
$x := \{x_i\},(i=1...n)$
ということである。

完全データ尤度の計算

この時仮に確率変数 $Z$ の実現値 $z$ も取得できたと仮定し、その時の尤度を完全データ尤度と呼ぶ事にし、計算してやると
$L^{c}(\theta|X=x,Z=z)=\prod_{i=1}^{n} P(X_i=x_i,Z_i=z_i|\theta)= \prod_{i=1}^{n} P(X_i=x_i|Z_i=z_i,\theta)P(Z_i=z_i|\theta)$
ここで

$P(X_i=x_i|Z_i=z_i,\theta)=\left$z_ig(x_i) + (1-z_i)h(x_i)\right$$
$P(Z_i=z_i|\theta)=\theta^{z_i}(1-\theta)^{1-z_i}$

であるので( $z_i=1,0$ を代入してみれば明らか)代入すると
$L^{c}(\theta|X=x,Z=z)=\prod_{i=1}^{n}\left$z_ig(x_i) + (1-z_i)h(x_i)\right$ \theta^{z_i}(1-\theta)^{1-z_i}$
と表わすことができる*1。
（ここが設問aの答え）

EMアルゴリズムの構築

$\theta$ というパラメーターの推定を最尤推定の枠組みで考えた場合、最大化すべき量は
$\log L(\theta|X=x) = P(X=x|\theta)=\prod_{i=1}^n P(X_i=x_i|\theta)$
であるが、ベイズの定理を用いて
$P(X=x|\theta)=\frac{P(X=x,Z=z|\theta)}{P(Z=z|X=x,\theta)}$
となるので、両辺 $log$ を取って確率を尤度としてみてやると
$\log L(\theta|X=x)=\log L^{c}(\theta|X=x,Z=z) - \log L(X=x,\theta|Z=z)$
とする事が出来る。さらに両辺に $P(Z=z|\hat{\theta},X=x)$ を掛けて $z$ で積分してやると左辺は $z$ に依存しないのでそのままになり
$\log L(\theta|X=x)=\mathbb{E}_{\hat{\theta}} \left[\log L^{c}(\theta|X=x,Z)\right] - \mathbb{E}_{\hat{\theta}} \left[ \log L(X=x,\theta|Z) \right]$
とすることができる。EMアルゴリズムはこの右辺第一項を最大化するアルゴリズムである*2。この手法を使うご利益としては、通常の最尤推定で扱う尤度関数が解析的に扱いにくい場合に隠れ変数を導入する事で尤度関数の計算が解析的に出来るケースへ還元することが出来るといったメリットがある。

EMアルゴリズムのその手順を書くと

１：初期値 $\hat{\theta}_{(0)}$ を選択, $m=0$ と設定
２：Eステップ
$Q(\theta|\hat{\theta}_{(m)}, x) = \mathbb{E}_{\hat{\theta}_{(m)}} \left[\log L^{c}(\theta|X=x,Z)\right]$
を計算する。期待値は $P(Z=z|X=x,\hat{\theta}_{(m)})$ として確率変数Zに対して取る
３：Mステップ
$\hat{\theta}_{(m+1)} = {\rm arg\max_{\theta}} Q(\theta|\hat{\theta}_{(m)},x)$
$m = m+1$
とする
４：２〜３のステップを指定したレベルに収束するまで繰り返す。

と記述されるものである。数値計算を使わないで解析的に各ステップを評価する場合、あらかじめ

$\mathbb{E}_{\hat{\theta}_{(m)}} \left[\log L^{c}(\theta|x,Z)\right]$ ...(A)
${\rm arg \max_{\theta}} Q(\theta|\hat{\theta}_{(m)},x)$ ...(B)

の計算しておかなければならないのでやる。

(A)の計算

$\mathbb{E}_{\hat{\theta}_{(m)}} \left[\log L^{c}(\theta|X=x,Z)\right] =\mathbb{E}_{\hat{\theta}_{(m)}} \left[ \sum_{i=1}^n \log \left$\left\(Z_ig(x_i) + (1-Z_i)h(x_i)\right$ \theta^{Z_i}(1-\theta)^{1-Z_i}\right\)\right]$
( $Z_i$ が1か0しか取らないという事実より）
$=\mathbb{E}_{\hat{\theta}_{(m)}} \left[ \sum_{i=1}^n \log \left$\left\(g(x_i)^{Z_i}h(x_i)^{(1-Z_i)}\right$ \theta^{Z_i}(1-\theta)^{1-Z_i}\right\)\right]$
$=\mathbb{E}_{\hat{\theta}_{(m)}} \left[ \sum_{i=1}^n \left\{ Z_i\log$g(x_i)$+(1-Z_i)\log$h(x_i)$+Z_i\log(\theta)+(1-Z_i)\log(1-\theta) \right\} \right]$
$=\mathbb{E}_{\hat{\theta}_{(m)}} \left[ \sum_{i=1}^n \left\{ Z_i\log\left(\frac{g(x_i)\theta}{h(x_i)(1-\theta)}\right\)+\log\left$h(x_i)(1-\theta)\right$ \right\}\right]$
$= \sum_{i=1}^n \left\{\log\left(\frac{g(x_i)\theta}{h(x_i)(1-\theta)}\right\) \mathbb{E}_{\hat{\theta}_{(m)}} \left[Z_i\right]+\log\left$h(x_i)(1-\theta)\right$\right\}$ ...(C)
ここでベイズの定理から
$P(Z_i=z_i|X_i=x_i,\theta) = \frac{P(Z_i=z_i,\theta)}{P(X_i=x_i,\theta)}P(X_i=x_i|Z_i=z_i,\theta)=\frac{\theta^z_i (1-\theta)^z_i}{ \theta g(x_i) + (1-\theta) h(x_i)}(z_ig(x_i)+(1-z_i)h(x_i)),(1=1...n)$
なので
$\mathbb{E}_{\hat{\theta}_{(m)}} \left[Z_i\right] = P(Z_i=1|x,\hat{\theta}_{(m)})\times 1+P(Z_i=0|x,\hat{\theta}_{(m)})\times 0 = \frac{\hat{\theta}_{(m)} g(x_i)}{\hat{\theta}_{(m)} g(x_i) + (1-\hat{\theta}_{(m)}) h(x_i)}$ ...(D)
従って(D)を(C)に代入する事で、(C)は
$= \sum_{i=1}^n \left\{ \log\left(\frac{g(x_i)\theta}{h(x_i)(1-\theta)}\right\)\frac{\hat{\theta}_{(m)} g(x_i)}{\hat{\theta}_{(m)} g(x_i) + (1-\hat{\theta}_{(m)}) h(x_i)}+\log\left$h(x_i)(1-\theta)\right$\right\}$
となる。
$\therefore \mathbb{E}_{\hat{\theta}_{(m)}} \left[\log L^{c}(\theta|X=x,Z)\right] = \sum_{i=1}^n \left\{ \log\left(\frac{g(x_i)\theta}{h(x_i)(1-\theta)}\right\)\frac{\hat{\theta}_{(m)} g(x_i)}{\hat{\theta}_{(m)} g(x_i) + (1-\hat{\theta}_{(m)}) h(x_i)}+\log\left$h(x_i)(1-\theta)\right$\right\}$ ...(E)
（ここが設問bの答え）

(B)の計算

$Q(\theta|\hat{\theta}_{(m)},x)=\mathbb{E}_{\hat{\theta}_{(m)}} \left[\log L^{c}(\theta|X=x,Z)\right]$ なので(B)である ${\rm arg \max_{\theta}} Q(\theta|\hat{\theta}_{(m)},x)$ を計算するためには(E)を最大化するような $\theta$ を見つければよい。従って(E)の右辺を $\theta$ で偏微分し、それが0となるような $\theta$ を探す。
$\frac{\partial}{\partial \theta}\sum_{i=1}^n \left\{ \log\left(\frac{g(x_i)\theta}{h(x_i)(1-\theta)}\right\)\frac{\hat{\theta}_{(m)} g(x_i)}{\hat{\theta}_{(m)} g(x_i) + (1-\hat{\theta}_{(m)}) h(x_i)}+\log\left$h(x_i)(1-\theta)\right$\right\}$
$= \frac{\partial}{\partial \theta}\sum_{i=1}^n \left\{ \left(\log\left(g(x_i)\theta\right\) - \log\left(h(x_i)(1-\theta)\right\)\right\)\frac{\hat{\theta}_{(m)} g(x_i)}{\hat{\theta}_{(m)} g(x_i) + (1-\hat{\theta}_{(m)}) h(x_i)}+\log\left$h(x_i)(1-\theta)\right$\right\}$
$=\sum_{i=1}^n \left\{\left(\frac{1}{\theta} + \frac{1}{1-\theta}\right\)\frac{\hat{\theta}_{(m)} g(x_i)}{\hat{\theta}_{(m)} g(x_i) + (1-\hat{\theta}_{(m)}) h(x_i)} -\frac{1}{1-\theta} \right\}$
$=\sum_{i=1}^n \frac{1}{\theta(1-\theta)} \left( \frac{\hat{\theta}_{(m)} g(x_i)}{\hat{\theta}_{(m)} g(x_i) + (1-\hat{\theta}_{(m)}) h(x_i)} - \theta\right\) =0$
$\therefore \theta = \frac{1}{n} \sum_{i=1}^n \frac{\hat{\theta}_{(m)} g(x_i)}{\hat{\theta}_{(m)} g(x_i) + (1-\hat{\theta}_{(m)}) h(x_i)}$
この $\theta$ に関する更新の式がEMアルゴリズムでいう「３：Mステップ」に対応する。今回の場合、「２：Eステップ」は式(A)の計算として実行してはいるものの、実際のプログラムの中では必要ない。

EMアルゴリズムの実装

あとは上で計算した数式をコードに落とし込むだけとなって、ここでは参照している練習問題5.14に合わせて
$\phi(x)=\frac{1}{\sqrt{2\pi}} \exp^{-0.5 x^2}$ （標準正規分布の確率密度関数）
$h(x)=\phi(x)$ （標準正規分布に設定）
$g(x)=\frac{\phi\left(\frac{x-2}{2}\right)}{2}$ （平均２・標準偏差２の正規分布に設定）
$\theta=0.3$
$n=25$
と設定した。よくある混合ガウシアンに対応。真のパラメータ $\theta=0.3$ への収束の様子をグラフにしてみると

(縦軸：パラメーター $\theta$ の推定値・横軸：EMアルゴリズムのループ回数）
という感じでだいたい10回もE-Mステップを繰り返せば収束としてはよい感じか。あと思った以上にサンプルが少なくて(25)もちゃんと動くんだなということがわかった。同条件で何度かシミュレーションを実行すると推定値自体は大体0.1のオーダーでばらついてしまうのでできるならもっとサンプル数を増やしておくべき所ではあるという結論。
（ここが設問cの答え）