トップ > 統計科学

逆ガンマ分布（事後分布）〜正規分布（尤度関数）×逆ガンマ分布（事前分布）

統計科学

一般に、ある確率測度\mathbb{P}の下で、逆ガンマ分布に従う確率変数Xの確率密度関数 f(x; \alpha, \beta)は
f(x; \alpha, \beta) = \frac{\beta^\alpha}{\Gamma(\alpha)} x^{-\alpha - 1}\exp\left\{ -\frac{\beta}{x}\right\}
である。

この時、確率変数Xを分散に持つ正規分布N(\mu, X)を尤度関数とし、逆ガンマ分布 f(x; \alpha_0, \beta_0)を事前分布とすると、
確率変数Xの事後確率密度関数は \tilde{f}(x; \alpha, \beta)

\tilde{f}(x; \alpha, \beta) \propto \frac{1}{\sqrt{2\pi}x} \exp\left\{ -\frac{(y-\mu)^2}{2x}\right\} \frac{\beta_0^{\alpha_0}}{\Gamma(\alpha_0)} x^{-\alpha_0 - 1}\exp\left\{-\frac{\beta_0}{x}\right\} \propto \frac{1}{x} \exp\left\{ -\frac{(y-\mu)^2}{2x}\right\} x^{-\alpha_0 - 1}\exp\left\{-\frac{\beta_0}{x}\right\} \propto x^{-\alpha_0 - 2} \exp\left\{ -\frac{1}{x}\left( \beta_0 + \frac{1}{2}(y-\mu)^2\right)\right\}
従って、
\alpha = \alpha_0 +1
\beta = \beta_0 + \frac{1}{2}(y-\mu)^2
となり、 \tilde{f}(x; \alpha, \beta)のパラメーターが決定され、かつ、その確率分布自体は逆ガンマ分布となる。すなわち自然共役である。

参考

正規分布（事後分布）〜正規分布（尤度関数）×正規分布（事前分布）

統計科学

一般に、ある確率測度\mathbb{P}の下で、正規分布に従う確率変数Xに対し、

  • 尤度関数：X \sim \mathcal{N}(\mu_1, \sigma_1)
  • 事前分布：X \sim \mathcal{N}(\mu_0, \sigma_0)

であることを仮定したとき、事前分布が共役事前分布となっていることから、事後分布も正規分布 \mathcal{N}(\hat{\mu}, \hat{\sigma})となり、

  • \frac{1}{\hat{\sigma}^2} = \frac{1}{\sigma_1^2} + \frac{1}{\sigma_0^2}
  • \hat{\mu} = \frac{\hat{\sigma}^2}{\sigma_1^2} \mu_1 + \frac{\hat{\sigma}^2}{\sigma_0^2} \mu_0

が成立する。ただしここで、\mathcal{N}(\mu, \sigma)は平均\mu, 分散\sigmaを持つ正規分布を表す。従って、データが N \in \mathbb{Z}個存在する場合には、上式を再帰的に用いることで

  • \frac{1}{\hat{\sigma}^2} = \sum_{i=1}^{N} \frac{1}{\sigma_i^2} + \frac{1}{\sigma_0^2}
  • \hat{\mu} = \sum_{i=1}^{N} \frac{\hat{\sigma}^2}{\sigma_i^2} \mu_i + \frac{\hat{\sigma}^2}{\sigma_0^2} \mu_0

が成立する。

やってみよう分析！Rで強化学習(Q-learning, ε-greedy行動選択)

R 統計科学

のR実装版。強化学習自体の解説は上の記事読んどいたらいい。めんどいのでとりあえずε-greedyのみやった。計算結果は

> Qlearning()
     [,1]     [,2]
[1,]    5 20.00000
[2,]   10  4.99903

となって、上のLINK先と同じなのでコードは間違ってなさそうだ。

以下、全コード。めんどいのでノーコメント。後で昔の俺が未来の俺の首を絞める可能性大だ。

#行動選択
selectAction <- function(s, numA, Qt)
{
  qa <- Qt[s,]
  max_indexes <- (1:length(qa))[qa==max(qa)]
  if(length(max_indexes) == 1){
    max_indexes
  }else{
    max_indexes[sample(length(max_indexes), 1)]
  }
}
epsilonGreedy <- function(epsilon, numA, s, Qt)
{
  if(runif(1) < epsilon)
  {
    sample.int(numA, 1)
  }else{
    selectAction(s, numA, Qt)
  }
}
nextState <- function(s, a)
{  
  ifelse(a==1, ifelse(s==1, 2, 1), s)
}
calcReward <- function(s, a, net)
{
  ifelse(a!=1 && s==1, net, 0)
}
Qlearning <- function()
{
  numA <- 2
  numS <- 2
  alpha <- 0.3
  gamma <- 0.5
  epsilon <- 0.1
  trialMax <- 10000
  stepMax <- 10
  net <- 10
  s = 1
  Qt <- matrix(0, numS, numA)
  
  for(i in 1:trialMax)
  {
    for(j in 1:stepMax)
    {
      a <- epsilonGreedy(epsilon, numA, s, Qt)
      sd <- nextState(s, a)
      reward <- calcReward(s, a, net)
      Qt[s, a] <- (1 - alpha)*Qt[s, a] + alpha*(reward + gamma*max(Qt[sd,]))

      if(reward > 0){
        s <- 1
        break
      } else{
        s <- sd        
      }
    }
  }
  Qt
}

逐次モンテカルロ/(粒子|パーティクル|モンテカルロ)フィルタを実装してみた

R 統計科学

このポストの概要

  • 逐次モンテカルロ法 (Sequential Monte Carlo: SMC)/粒子フィルタ(Particle Filter)は、状態空間モデルの状態変数の系列 x_t (t=0,1,\dots T)を観測値の系列 y_t (t=0,1,\dots T) のみから推定するアルゴリズム
  • パッケージを使ってもいいんだど、お勉強も兼ねて自分でコード書いてみましたというお話(コアの部分だけならRで30行弱)
  • コードは固定ラグ平滑化にまで対応(自己組織化 or フルベイズでのパラメータ推定系の機能はなし）
  • 状態空間モデルの細かい話は適当な教科書読みましょう

逐次モンテカルロ/粒子(パーティクル)フィルタとは

逐次モンテカルロ法 (Sequential Monte Carlo: SMC)/粒子フィルタ(Particle Filter)は、線形状態空間モデルに対してはカルマンフィルタを使うように、非線形状態空間モデルに対して状態変数の推定を行うアルゴリズムです。具体的には状態変数に対する確率分布をモンテカルロ法で生成したサンプルで近似する手法です。更なる別名としてSampling/Importance resampling (SIR)とも呼ばれているようです。またまた、Sequential Importance Sampling(SIS)なる別のアルゴリズムもあって、これは逐次モンテカルロ法における"リサンプリング処理"というモンテカルロで生成したサンプルに対するリサンプリング処理がない版になります(参照：粒子フィルタ - Wikipedia、英語版のほうがいいかも)。

名称が多数あってややこしいので、以下ではSMCに統一する方向で。

Rでの実装はあるんかい？

Rから使えそうなSMCの実装としては

あたりがある。なお、正確にはRcppSMCはC++のライブラリに処理をブン投げるという意味でRでの実装ではないです。またSMCパッケージは３年前に更新が止ってるのでアレ感ありますね、アレ感。

SMCを含めた状態空間モデルの平易なテキストとしては

が超お勧め。6章に粒子フィルタの解説が載っており、ここのコードもだいたいそれ見て実装してる。


また、特に(線形)状態空間モデルについては、以下のスライドがまとまっていて、大変ありがたいのでこれも見ておくといいかと。

また、このスライドの中で説明されているdlmパッケージについては、書籍

の説明がかなり詳しい。


・・・で、私がお勉強用に作ったSMCの実装のコアの部分は以下(particle.filter関数)。コメント含め28行です。短く書けるのは良いことです。
一応、多次元系列データも扱えるように作ってはいるが、ちゃんと試してはいない。

particle.filter <- function(x0, size.particle, size.dim, size.data, system.equation, likelihood, lag=0)
{
  total.loglikelihood <- 0
  #dimension index : paricle * dimension * lag
  dims <- c(size.particle, size.dim, lag+1)
  x0 <- array(c(rep(x0, each=size.particle),rep(NA, size.dim*size.particle*lag)), dims)
  x  <- array(rep(NA, size.particle*size.dim*(lag+1)), dims)
  dimnames(x0) <- make.name(size.particle, size.dim, lag)
  dimnames(x)  <- make.name(size.particle, size.dim, lag)
  states <- vector("list", size.data)
  for( t in 1:size.data)
  {
    #Prediction : p(x_{t}|x_{t-1})
    for(index.particle in 1:size.particle)
    {
      x[index.particle,, 1] <- system.equation(x0[index.particle,,1])
      x[index.particle,,-1] <- x0[index.particle,,-(lag+1)]
    }
    #Likelihood : p(y_{t}|y_{1:t})
    w <- apply(x, 1, function(z){likelihood(t, z[,1])})
    total.loglikelihood <- total.loglikelihood + log(sum(w)/size.particle)
    #Weight ' resampling
    index <- resampling(w/sum(w))
    #Filtering : p(x_{t}|y_{t})
    x0 <- x[index,,,drop=FALSE]
    states[[t]] <- make.state(t, w, x, x0)
  }
  list(loglikelihood=total.loglikelihood, size=c(particle=size.particle, data=size.data, dim=size.dim,lag=lag), states=states)
}

実行結果

とりあえず正しく動作しているのかを確認したかったので、答え合わせのしやすい線形状態空間モデルの例として以下のモデル
状態方程式： x_t = x_{t-1} + v_t, v_t \sim N(0, (\alpha*\sigma)^2)
観測方程式： y_t = x_t + w_t, w_t \sim N(0, \sigma^2)
を使用。パラメーターとしてここでは \alpha=0.8, \sigma=1.0と設定してます。

このモデルをRで書くと以下のようになって、モデル固有な部分はsystem.equation関数とlikelihood関数に全部押しつけるように設計してます。また、lag<-10となっている箇所は、固定ラグ平滑化の固定ラグのサイズ指定に相当します。つまり、固定ラグ平滑化のラグは10をMAXとして取っているということです。

# x_t = x_{t-1} + v_t, v_t \sim N(0, (\alpha*\sigma)^2)
# y_t = x_t + w_t, w_t \sim N(0, \sigma^2)
#という状態空間モデルの生成
make.system.equation <- function(alpha, sigma)
{
  function(x)
  {
    v <- rnorm(length(x), sd=alpha*sigma)
    x + v
  }
}
make.likelihood.function <- function(y, sigma)
{
  function(t, x)
  {
    1/(sqrt(2*pi)*sigma)*exp(-(y[t,]-x)^2/(2*sigma^2))
  }
}
sigma <- 1.0
alpha <- 0.8
set.seed(100)
#データは100要素をもつ1系列として設定
size.data <- 100
#1000粒子用意
size.particle <- 1000
#真の状態変数系列xを作成
x.true <- cumsum(alpha*sigma*rnorm(size.data))
#そこにノイズをのっけて観測系列yを作成
y <- matrix(sigma*rnorm(size.data)+x.true)
#状態方程式＆観測方程式（尤度で表現）を生成
system.equation <- make.system.equation(alpha, sigma)
likelihood      <- make.likelihood.function(y, sigma)
#SMCを適用
lag <- 10
pf <- particle.filter(rnorm(1), size.particle, 1, size.data, system.equation, likelihood, lag=lag)

粒子ごとに状態変数xの推定値が違うので、この結果をなんらかの手段(平均など)を用いて集約せんといかんわけです。そこで、各時点ごとの集約を実行するための関数としてaggregate.pf関数を用意したんでそれを使うことにします。この関数は、デフォルトでは各時点での粒子の状態の平均値を計算するようになってます。

#各粒子の算出した状態変数を集約(平均)
x.pf     <- aggregate.pf(pf, "filter", lag=0)
x.pf.lag <- aggregate.pf(pf, "filter", lag=lag)

この結果（ラグなし＆10ラグの固定ラグ平滑化）を描画すると以下のようになります。
ここでラグ付の結果を調整して通常のフィルタリングと時点を合わせるために適当な処理(c(x.pf.lag[-(1:lag)], rep(NA, lag))))が入っています。

matplot(cbind(x.pf, c(x.pf.lag[-(1:lag)], rep(NA, lag))), type="l",lty=1)

更にこれらを真の状態変数(x.true)と重ねて描画すると

matplot(cbind(x.true, x.pf, c(x.pf.lag[-(1:lag)], rep(NA, lag))), type="l",lty=1)
legend("topleft", c("X(true)", "X(filter)", "X(fixed lag)"), col = c("black", "red", "green"), lty=1)


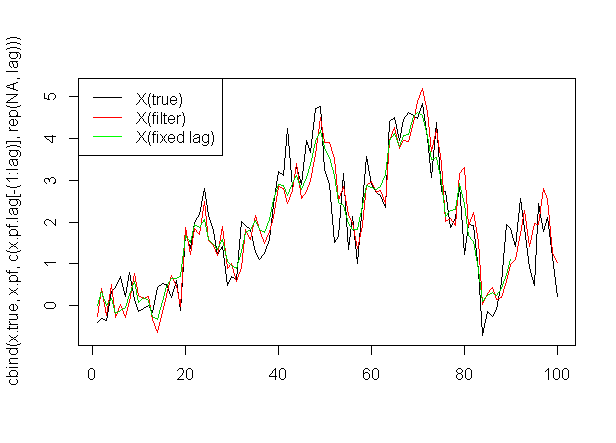
という感じ。あってる・・・？のかは判断しにくいので別の手段を考えます。

これがある程度妥当な結果かどうか確かめるため、ここで作成したモデルは線形状態空間モデル＋ノイズはガウシアンってことで、カルマンフィルタでも計算できるので昔メモっといたカルマンフィルタの記事にならって、FKFパッケージってのを使って同じモデルのフィルタリングを実行してみる。カルマンフィルタのパッケージにどういうのがあるのかを知りたい場合には上述のスライドを見るか、State Space Models in R(PDF)を読むとよい。これを読む限りFKFはマイナーパッケージぽいが、まぁ答え合わせに使う分にはいいだろと。

同モデルをFKFパッケージのカルマンフィルタにかけるには以下のように書く。

#カルマンフィルタとの比較
library(FKF)
dt <- matrix(0)
ct <- matrix(0)
Zt <- matrix(1)
Tt <- matrix(1)
a0 <- 0
P0 <- matrix(0.01)
fkf.obj <- fkf(a0, P0, dt, ct, Tt, Zt, HHt=matrix((alpha*sigma)^2), GGt=matrix(sigma^2), yt = t(y))

この結果をSMCの結果とあわせて描画してみると

plot(y)
lines(fkf.obj$att[1, ], col = "blue")
lines(x.pf, col = "red")
legend("bottomright", c("original data", "filter(Kalman)", "filter(PF)"),  col = c("black", "blue", "red"), lty=1)


赤線(SMC)と青線(カルマンフィルタ)がほぼ重なっており、俺俺SMC実装は合っていそうだなということがわかる。やったね！

Rの全コード

とりあえずGistにUPしておいた。そのうちまとめるかも？

その他の参考スライド

特に@xiangze氏のスライドに関してはGitHub - xiangze/particlefilter_dynamical: particle filter sample of dynamical systems in Rに実装がアップされているので、こちらも勉強になる。また、@berobero11氏のBLOGポストはRStanを活用しつつ、さきほど紹介したテキスト「予測にいかす統計モデリングの基本」の内容を忠実に再現したものなので一読の価値あり。また、数式数式したい方は中野/北川先生の資料を見るといいんじゃなかろうか。

ブラウン橋(Brownian bridge)作りたい

R 統計科学 金融工学

簡単なんだけど、やってなかったなって。ブラウン橋言ってる人もいるし、ブラウニアン橋いってる人もいてどっちが正しいのかわかんねぇけど、ここではブラウン橋でいく。

ブラウン橋は、W(t)を標準ブラウン運動として
B_t := W_t - t W_1,\;t \in [0,1]
と書かれる確率過程B(t)だと思っておけばいい。こいつの平均値は0で、分散は t(1-t)となる。で、実際にRでやってみましょうと。

このブラウン橋を生成する関数は以下。

bb <- function(size.path, size.timestep)
{
  result <- matrix(0, nrow=size.path, ncol=size.timestep+1)
  dt <- 1/size.timestep
  for(i in 1:size.path)
  {
    z <- cumsum(rnorm(size.timestep))*sqrt(dt)
    result[i,] <- c(0, z - (1:size.timestep)/size.timestep*z[length(z)])
  }
  result
}

実際に走らせてみると、まぁ0.5時点での標準偏差がだいたい0.5になってるので、あってるだろうと。

> size.path <- 10^3
> size.timestep <- 10^2
> x <- bb(size.path, size.timestep)
> sd(x[,size.timestep/2])
[1] 0.5078946
> matplot(t(x[1:100,]), type="l")

描画させたmatplotの結果が以下。

また、このブラウン橋と同じ確率分布となる確率過程は以下のように書ける。
dY_t := -\frac{Y_t}{1-t}dt + dW_t ,\;t \in [0,1], Y_0=0
B_tはブラウン運動W_tの作るσ加法族の\mathcal{F}_t可測とはならないけど、こちらは\mathcal{F}_t可測になる点が異なる。

この確率微分方程式をベースに、ブラウン橋を生成する関数は以下。

bb2 <- function(size.path, size.timestep)
{
  result <- matrix(0, nrow=size.path, ncol=size.timestep+1)
  for(i in 1:size.path)
  {
    dt <- 1/size.timestep
    z <- rnorm(size.timestep)*sqrt(dt)
    x <- rep(0, size.timestep+1)
    for(j in 1:size.timestep)
    {
      x[j+1] <- x[j] + -x[j]/(1-(j*dt))*dt + z[j] 
    }
    result[i,] <- x
  }
  result
}

実際に走らせてみると、こちらも0.5時点での標準偏差がだいたい0.5になってるのであってそうだ。

> size.path <- 10^3
> size.timestep <- 10^2
> y <- bb2(size.path, size.timestep)
> sd(y[,size.timestep/2])
[1] 0.5296784
> matplot(t(y[1:100,]), type="l")

描画させたmatplotの結果が以下。

この話をパッケージ使ってやるなら、ウィーン工科大の雑多な関数パッケージである「e1071」パッケージ中にあるrbridge 関数使うとよい。
パスは一本しか出ない。

> library(e1071)
> x <- rbridge()
> plot(x,type="l")


参考

AR(1)モデルのメモ

R 統計科学

今更感あるが、諸事情によりメモ。やりたいことは(定常性を仮定した)AR(1)モデルの自己相関係数がちゃんと理論値と一致するのかを見たいって話。

AR(1)モデルとは

AR(1)は、適当な確率過程 x=\{x_t; t\ge 1 \}が、
x_t=d+\rho x_{t-1} + \eta_t
に従うようなモデル。ここで、

  • \eta_tは独立な平均0、標準偏差\sigmaの正規分布、dは適当な定数
  • \{x_t; t\ge 1 \}に(弱)定常性を仮定(AR(1)に関しては|\rho| < 1が条件)

としておく。この時、その平均値 E(x_t)と分散Var(x_t)は時間tに依らずに一定となりそれぞれ

  • E(x_t)=d/(1-\rho)
  • Var(x_t) = \sigma^2/(1-\rho^2)

となる。

標本自己相関関数 \gamma_hは、標本自己共分散C_h

  • C_h=\frac{1}{T}\sum^{T}_{t=h+1}\left(x_t-\mu\right)\left(x_{t-h}-\mu\right)
  • \mu=\frac{1}{T}\sum_{t=1}^{T} x_t (標本平均)

を用いて

  • \gamma_h = \frac{C_h}{C_0

で定義される。特に、AR(1)モデルの場合、 \gamma_hの関数系をちゃんと計算することが出来て、

  • \gamma_h = \rho^{h}

になる。ちゃんとこうなるのかをシミュレーションを通して確かめることが目的。

Rでやりたい

arima.sim関数を使ってもいいが、AR(1)のシミュレーションぐらいならサクっと

AR1 <- function(size, d, rho, sigma)
{
  Reduce(function(x, noise){d+rho*x+noise}, rnorm(size, mean=0, sd=sigma), init=d/(1-rho), accumulate=TRUE)
}

こんな感じで関数を用意できるので、こいつを使うことにする。
まずは、適当なパラメーターに対して100万個のデータxを生成。この時x_1に相当するもの(init引数)は、平均値になるようにAR1関数内で調整している。

rho <- 0.8
sigma <- 0.5
d <- 1
x <- AR1(10^6, d, rho, sigma)

生成したデータxの標本平均が理論値と合うかのチェック。ほぼ合ってますよと。

> mean(x)
[1] 5.001267
> d/(1-rho)
[1] 5

同じくデータの標本分散が理論値と合うかチェック。こちらもほぼ合ってますよと。

> var(x)
[1] 0.6930294
> sigma^2/(1-rho^2)
[1] 0.6944444

最大のラグを30とした場合の自己相関を計算し、合わせて描画も行う。ちなみにacf関数のplot引数をfalseと設定すると描画はされない。

lag <- 30
x.acf <- acf(x, lag.max = lag)$acf

これが理論的な自己相関と一致するかを描画して比較してみる。結果はたしかにそれっぽくは見える。

matplot(cbind(x.acf, rho^(0:lag)), type="l")

こういう指数関数ぽい形になっている関数はlogを取って線形に変換( h\log(\rho))した方が比較しやすいので、logを取ってもう一度描画。
ラグ30あたりの端以外はまぁいい感じか。

matplot(cbind(log(x.acf), (0:lag)*log(rho)), type="l")


参考

scikit-learnでサポートベクトル回帰、及びそのパラメーター推計 with クロスバリデーションやってみる

python 統計科学

サポートベクトル回帰(Support Vector Regression, SVR)の理論が大体脳内整理出来たので、実践もしたいぞと、そしてちょいとpythonを使う別件があるので、慣れの意味も込めてR言語ではなくpythonとその機械学習ライブラリであるscikit-learnを使ってやるぞとそういうことです。

scikit-learn自体のインストールはこの記事の最下部にある日本語のLINKを見れば良いと思う。
俺はpip使ってインストールしたような気がするけど、なにぶんずいぶんと昔なので忘れてしまった。pipで入れるなら

pip install scikit-learn

でOK。裏でコンパイルが走っていたような記憶があるので、C++のコンパイラいれておかないとだめかも。
windows用のバイナリファイルだと

にあるので、お手元のpythoのバージョンに合わせて入れちゃえばよさげ。

お試しの例題として用いるもの

ここでの例は
- -πからπまでの範囲のsin関数+noise
なデータ、つまり y=sin(x)+noise, x \in \left[ -\pi, \pi \right] を満たすような(x,y)の組に対してサポートベクトル回帰をかますこととする。
データの作成法は、 \left[ -\pi, \pi \right] の区間から複数個一様にサンプリングした後、それをsin関数に食わせてノイズ(ここでは平均0,分散0.01ガウシアン)を乗せてyとした。
図示しておくと

なデータ(x,yのペア)が与えられているというシチュエーションを考えている。ここで言及した元データ＆グラフは以下のスクリプトで作成。

import numpy as np
import matplotlib.pyplot as plt
# X座標を適当にサンプリングして指定、それに合わせてy = sin(x) + noiseを生成
np.random.seed(1)
x = np.sort(np.random.uniform(-np.pi, np.pi,100))
y = np.sin(x) + 0.1*np.random.normal(size=len(x))
# scikit-learnに突っ込むためにフォーマット変更
x = x.reshape((len(x),1))
# 全データの描画
plt.plot(x, y, 'o')
plt.show()

サポートベクトル回帰(SVR)の実行

サポートベクトル回帰はscikit-learnにあるSVR関数を用いて実行する。上で作成した元々のデータを6:4の比率でトレーニング＆テストデータに分けて使用。

SVRの戻り値はsklearn.svm.classes.SVRクラスのオブジェクトになってて、こいつのpredictメソッドで予測、scoreメソッドで”予測のあてはまり度合い”を表す決定係数R^2を取得する事ができる*1
このオブジェクトについての詳細は

を見るべし。実際にトレーニングデータから学習した結果を使ってテストデータに対する当てはめを行ってみると

という感じになる(赤が予測で青が実際)。

コードは以下。
SVR関数にx,yを食わせる際、yをN次元のベクトルとした場合、xは1次元であろうとN×M次元の行列形式にしなければならない点に注意。

from sklearn import svm
from sklearn import cross_validation
#データを6割をトレーニング、4割をテスト用とする
x_train, x_test, y_train, y_test = cross_validation.train_test_split(x, y, test_size=0.4)
# 線でつないでplotする用にx_test・y_testをx_testの昇順に並び替える
index = x_test.argsort(0).reshape(len(x_test))
x_test = x_test[index]
y_test = y_test[index]
# サポートベクトル回帰を学習データ使って作成
reg = svm.SVR(kernel='rbf', C=1).fit(x_train, y_train)
# テストデータに対する予測結果のPLOT
plt.plot(x_test, y_test, 'bo-', x_test, reg.predict(x_test), 'ro-')
plt.show()
# 決定係数R^2
print reg.score(x_test, y_test)

クロスバリデーション(Cross Validation, CV)

今手元にあるトレーニングデータを更にK個に分割し、そのうちの1個をテストデータ(A)、残りK-1個を改めてトレーニングデータ(B)とし、(B)を用いてモデルを構築し、(A)に対して予測を行い、モデルの妥当性を検証する事を考える。分割したデータがK個あるので、テストデータの選び方自体もK通りあり、そのK個に分割されたトレーニングデータそれぞれをテストデータとしてK回検証を行い、得られたK回の結果(スコア、何らかのモデルの良し悪しを決める指標）を平均して1つの評価指標の推定値を得ることが出来、これをK-foldクロスバリデーションといいます。その詳細は

を読めば十分わかるかなと。
scikit-learnでは"回帰"に関してモデルの良し悪しを決める指標として

  • 決定係数R^2
  • 平均二乗誤差(Mean Squared Error, MSE)

を指定出来る*2が、ここでMSEの値は”通常の(統計学|機械学習)”でいうMSEの値が-1倍されたものであり、これがスコアとして返ってくる点に気を付ける*3。

これをscikit-learn使って書くと以下のようになる。

# 5-foldクロスバリデーション。デフォルトはr^2がスコアとなって返ってくる。すなわち以下と等価
# cross_validation.cross_val_score(svm.SVR(), x, y, cv=5, scoring="r2")
scores = cross_validation.cross_val_score(svm.SVR(), x, y, cv=5)
# 5-foldクロスバリデーション毎のR^2の平均値とその±2σレンジ
print("R^2(not adjusted): %0.2f (+/- %0.2f)" % (scores.mean(), scores.std() * 2))
#平均二乗誤差(MSE)をスコアに変更
scores = cross_validation.cross_val_score(svm.SVR(), x, y, cv=5, scoring="mean_squared_error")
# 5-foldクロスバリデーション毎のMSEの平均値とその±2σレンジ
print("MSE: %0.2f (+/- %0.2f)" % (-scores.mean(), scores.std() * 2))

クロスバリデーションとグリッドサーチを使ってSVRのパラメータを決める

単純にCVやるだけなら上でいいが、今まで所与だと思って放置していたモデルパラメータ、この例だと

  • 罰則の強さを表す:C
  • ガウシアンカーネルの広がりを表す:γ

を決めてやりたい。そのためにはGridSearchCV関数を用いる。
適当なパラメーターグリッド（組）に対してK-fold CV(ここでは5-fold）を繰り返し、スコア(ここではMSE)が最も良くなるパラメーターのSVRを出力する事ができる。
ちなみに以下のコードで

tuned_parameters = [{'kernel': ['rbf'], 'gamma': [10**i for i in range(-4,0)], 'C': [10**i for i in range(1,4)]}]

と書いている箇所を

tuned_parameters = [
    {'kernel': ['rbf'], 'gamma': [10**i for i in range(-4,3)], 'C': [10**i for i in range(-3, 4)]},
    {'kernel': ['linear'], 'C': [1, 10, 100, 1000]}
]

とすると、カーネルも同時に”パラメーター”として評価され、上記の通常言うようなパラメーターだけではなく、異なるカーネル間での結果比較も出来るのが素晴らしい*4。

このGridSearchCVを使って一番MSEがよくなるモデルを作成した結果が以下のグラフ。
「正答を青、最もMSEスコアの意味で(良|悪)いモデルの予測値を(赤|緑)」として示した。

コードは↓な感じ。一番スコアの良いモデルは

  • best_estimator_

というプロパティに格納されているので簡単に取得できるが、（普通は用途のない）一番スコアの悪いモデルを出すのに苦労した。

from sklearn.grid_search import GridSearchCV
#RBFカーネルのパラメーターγと罰則Cを複数個作ってその中で(スコアの意味で）良い物を探索(カーネルもパラメーターとして使用可能)
tuned_parameters = [{'kernel': ['rbf'], 'gamma': [10**i for i in range(-4,0)], 'C': [10**i for i in range(1,4)]}]
gscv = GridSearchCV(svm.SVR(), tuned_parameters, cv=5, scoring="mean_squared_error")
gscv.fit(x_train, y_train)
#一番スコア悪い&良い奴を出す
params_min,_,_ = gscv.grid_scores_[np.argmin([x[1] for x in gscv.grid_scores_])]
reg_min = svm.SVR(kernel=params_min['kernel'], C=params_min['C'], gamma=params_min['gamma'])
reg_max = gscv.best_estimator_
#全トレーニングデータを使って再推計
reg_min.fit(x_train, y_train)
reg_min.fit(x_train, y_train)
#正答(青)＆良い(赤)＆悪い(緑)の結果をPLOT
plt.plot(x_test, y_test, 'bo-',x_test, reg_max.predict(x_test), 'ro-',x_test, reg_min.predict(x_test), 'go-')
plt.show()

その他メモ

参考LINK

*1:なぜここでscoreメソッドが返す値として決定係数なのかはよくわかってない。SVRにおいて、決定係数があてはまりの良し悪しを判断するために使われる指標として普通なのだろうか???

*2:自作関数も可能。3.3. Model evaluation: quantifying the quality of predictions — scikit-learn 0.21.dev0 documentationを参照

*3:これはscikit-learnの仕様でmean_squared_error(MSE)関数をスコアとしてcross_val_score関数経由でCVやろうとすると、この関数内部で作られるscorerというスコア管理用のオブジェクトを作る際に使われるmake_scorer関数のgreater_is_better(値がでかい方がいい結果フラグ)引数が、MSEを使う場合false設定され、MSE自体の値が-1倍されるようになっている。make_scorer関数についてはsklearn.metrics.make_scorer — scikit-learn 0.19.2 documentationを参照

*4:ここではガウシアンカーネルと線形カーネルでの比較に相当